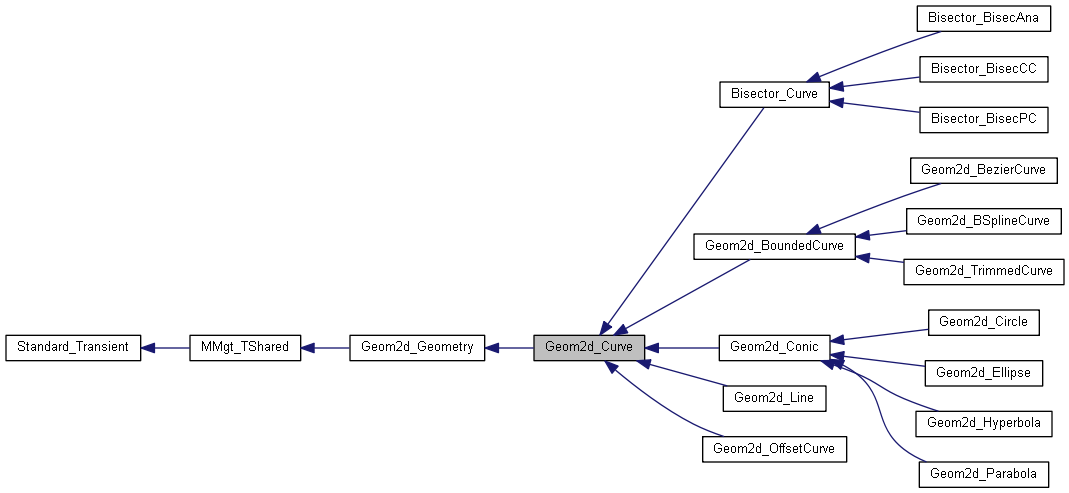
The abstract class Curve describes the common behavior of curves in 2D space. The Geom2d package provides numerous concrete classes of derived curves, including lines, circles, conics, Bezier or BSpline curves, etc. The main characteristic of these curves is that they are parameterized. The Geom2d_Curve class shows: More...
#include <Geom2d_Curve.hxx>
Public Member Functions | |
| virtual void | Reverse ()=0 |
| Changes the direction of parametrization of <me>. The "FirstParameter" and the "LastParameter" are not changed but the orientation of the curve is modified. If the curve is bounded the StartPoint of the initial curve becomes the EndPoint of the reversed curve and the EndPoint of the initial curve becomes the StartPoint of the reversed curve. More... | |
| virtual Standard_Real | ReversedParameter (const Standard_Real U) const =0 |
| Computes the parameter on the reversed curve for the point of parameter U on this curve. Note: The point of parameter U on this curve is identical to the point of parameter ReversedParameter(U) on the reversed curve. More... | |
| virtual Standard_Real | TransformedParameter (const Standard_Real U, const gp_Trsf2d &T) const |
| Computes the parameter on the curve transformed by T for the point of parameter U on this curve. Note: this function generally returns U but it can be redefined (for example, on a line). More... | |
| virtual Standard_Real | ParametricTransformation (const gp_Trsf2d &T) const |
| Returns the coefficient required to compute the parametric transformation of this curve when transformation T is applied. This coefficient is the ratio between the parameter of a point on this curve and the parameter of the transformed point on the new curve transformed by T. Note: this function generally returns 1. but it can be redefined (for example, on a line). More... | |
| Handle< Geom2d_Curve > | Reversed () const |
| Creates a reversed duplicate Changes the orientation of this curve. The first and last parameters are not changed, but the parametric direction of the curve is reversed. If the curve is bounded: More... | |
| virtual Standard_Real | FirstParameter () const =0 |
| Returns the value of the first parameter. Warnings : It can be RealFirst or RealLast from package Standard if the curve is infinite. More... | |
| virtual Standard_Real | LastParameter () const =0 |
| Value of the last parameter. Warnings : It can be RealFirst or RealLast from package Standard if the curve is infinite. More... | |
| virtual Standard_Boolean | IsClosed () const =0 |
| Returns true if the curve is closed. Examples : Some curves such as circle are always closed, others such as line are never closed (by definition). Some Curves such as OffsetCurve can be closed or not. These curves are considered as closed if the distance between the first point and the last point of the curve is lower or equal to the Resolution from package gp wich is a fixed criterion independant of the application. More... | |
| virtual Standard_Boolean | IsPeriodic () const =0 |
| Returns true if the parameter of the curve is periodic. It is possible only if the curve is closed and if the following relation is satisfied : for each parametric value U the distance between the point P(u) and the point P (u + T) is lower or equal to Resolution from package gp, T is the period and must be a constant. There are three possibilities : . the curve is never periodic by definition (SegmentLine) . the curve is always periodic by definition (Circle) . the curve can be defined as periodic (BSpline). In this case a function SetPeriodic allows you to give the shape of the curve. The general rule for this case is : if a curve can be periodic or not the default periodicity set is non periodic and you have to turn (explicitly) the curve into a periodic curve if you want the curve to be periodic. More... | |
| virtual Standard_Real | Period () const |
| Returns thne period of this curve. raises if the curve is not periodic. More... | |
| virtual GeomAbs_Shape | Continuity () const =0 |
| It is the global continuity of the curve : C0 : only geometric continuity, C1 : continuity of the first derivative all along the Curve, C2 : continuity of the second derivative all along the Curve, C3 : continuity of the third derivative all along the Curve, G1 : tangency continuity all along the Curve, G2 : curvature continuity all along the Curve, CN : the order of continuity is infinite. More... | |
| virtual Standard_Boolean | IsCN (const Standard_Integer N) const =0 |
| Returns true if the degree of continuity of this curve is at least N. Exceptions Standard_RangeError if N is less than 0. More... | |
| virtual void | D0 (const Standard_Real U, gp_Pnt2d &P) const =0 |
| Returns in P the point of parameter U. If the curve is periodic then the returned point is P(U) with U = Ustart + (U - Uend) where Ustart and Uend are the parametric bounds of the curve. More... | |
| virtual void | D1 (const Standard_Real U, gp_Pnt2d &P, gp_Vec2d &V1) const =0 |
| Returns the point P of parameter U and the first derivative V1. Raised if the continuity of the curve is not C1. More... | |
| virtual void | D2 (const Standard_Real U, gp_Pnt2d &P, gp_Vec2d &V1, gp_Vec2d &V2) const =0 |
| Returns the point P of parameter U, the first and second derivatives V1 and V2. Raised if the continuity of the curve is not C2. More... | |
| virtual void | D3 (const Standard_Real U, gp_Pnt2d &P, gp_Vec2d &V1, gp_Vec2d &V2, gp_Vec2d &V3) const =0 |
| Returns the point P of parameter U, the first, the second and the third derivative. Raised if the continuity of the curve is not C3. More... | |
| virtual gp_Vec2d | DN (const Standard_Real U, const Standard_Integer N) const =0 |
| For the point of parameter U of this curve, computes the vector corresponding to the Nth derivative. Exceptions StdFail_UndefinedDerivative if: More... | |
| gp_Pnt2d | Value (const Standard_Real U) const |
| Computes the point of parameter U on <me>. If the curve is periodic then the returned point is P(U) with U = Ustart + (U - Uend) where Ustart and Uend are the parametric bounds of the curve. More... | |
 Public Member Functions inherited from Geom2d_Geometry Public Member Functions inherited from Geom2d_Geometry | |
| void | Mirror (const gp_Pnt2d &P) |
| Performs the symmetrical transformation of a Geometry with respect to the point P which is the center of the symmetry and assigns the result to this geometric object. More... | |
| void | Mirror (const gp_Ax2d &A) |
| Performs the symmetrical transformation of a Geometry with respect to an axis placement which is the axis of the symmetry. More... | |
| void | Rotate (const gp_Pnt2d &P, const Standard_Real Ang) |
| Rotates a Geometry. P is the center of the rotation. Ang is the angular value of the rotation in radians. More... | |
| void | Scale (const gp_Pnt2d &P, const Standard_Real S) |
| Scales a Geometry. S is the scaling value. More... | |
| void | Translate (const gp_Vec2d &V) |
| Translates a Geometry. V is the vector of the tanslation. More... | |
| void | Translate (const gp_Pnt2d &P1, const gp_Pnt2d &P2) |
| Translates a Geometry from the point P1 to the point P2. More... | |
| virtual void | Transform (const gp_Trsf2d &T)=0 |
| Transformation of a geometric object. This tansformation can be a translation, a rotation, a symmetry, a scaling or a complex transformation obtained by combination of the previous elementaries transformations. (see class Transformation of the package Geom2d). The following transformations have the same properties as the previous ones but they don't modified the object itself. A copy of the object is returned. More... | |
| Handle< Geom2d_Geometry > | Mirrored (const gp_Pnt2d &P) const |
| Handle< Geom2d_Geometry > | Mirrored (const gp_Ax2d &A) const |
| Handle< Geom2d_Geometry > | Rotated (const gp_Pnt2d &P, const Standard_Real Ang) const |
| Handle< Geom2d_Geometry > | Scaled (const gp_Pnt2d &P, const Standard_Real S) const |
| Handle< Geom2d_Geometry > | Transformed (const gp_Trsf2d &T) const |
| Handle< Geom2d_Geometry > | Translated (const gp_Vec2d &V) const |
| Handle< Geom2d_Geometry > | Translated (const gp_Pnt2d &P1, const gp_Pnt2d &P2) const |
| virtual Handle< Geom2d_Geometry > | Copy () const =0 |
 Public Member Functions inherited from MMgt_TShared Public Member Functions inherited from MMgt_TShared | |
| virtual void | Delete () const override |
| Memory deallocator for transient classes. More... | |
 Public Member Functions inherited from Standard_Transient Public Member Functions inherited from Standard_Transient | |
| Standard_Transient () | |
| Empty constructor. More... | |
| Standard_Transient (const Standard_Transient &) | |
| Copy constructor – does nothing. More... | |
| Standard_Transient & | operator= (const Standard_Transient &) |
| Assignment operator, needed to avoid copying reference counter. More... | |
| virtual | ~Standard_Transient () |
| Destructor must be virtual. More... | |
| virtual const opencascade::handle< Standard_Type > & | DynamicType () const |
| Returns a type descriptor about this object. More... | |
| Standard_Boolean | IsInstance (const opencascade::handle< Standard_Type > &theType) const |
| Returns a true value if this is an instance of Type. More... | |
| Standard_Boolean | IsInstance (const Standard_CString theTypeName) const |
| Returns a true value if this is an instance of TypeName. More... | |
| Standard_Boolean | IsKind (const opencascade::handle< Standard_Type > &theType) const |
| Returns true if this is an instance of Type or an instance of any class that inherits from Type. Note that multiple inheritance is not supported by OCCT RTTI mechanism. More... | |
| Standard_Boolean | IsKind (const Standard_CString theTypeName) const |
| Returns true if this is an instance of TypeName or an instance of any class that inherits from TypeName. Note that multiple inheritance is not supported by OCCT RTTI mechanism. More... | |
| Standard_Transient * | This () const |
| Returns non-const pointer to this object (like const_cast). For protection against creating handle to objects allocated in stack or call from constructor, it will raise exception Standard_ProgramError if reference counter is zero. More... | |
| Standard_Integer | GetRefCount () const |
| Get the reference counter of this object. More... | |
| void | IncrementRefCounter () const |
| Increments the reference counter of this object. More... | |
| Standard_Integer | DecrementRefCounter () const |
| Decrements the reference counter of this object; returns the decremented value. More... | |
Additional Inherited Members | |
 Public Types inherited from Standard_Transient Public Types inherited from Standard_Transient | |
| typedef void | base_type |
| Returns a type descriptor about this object. More... | |
 Static Public Member Functions inherited from Standard_Transient Static Public Member Functions inherited from Standard_Transient | |
| static const char * | get_type_name () |
| Returns a type descriptor about this object. More... | |
| static const opencascade::handle< Standard_Type > & | get_type_descriptor () |
| Returns type descriptor of Standard_Transient class. More... | |
Detailed Description
The abstract class Curve describes the common behavior of curves in 2D space. The Geom2d package provides numerous concrete classes of derived curves, including lines, circles, conics, Bezier or BSpline curves, etc. The main characteristic of these curves is that they are parameterized. The Geom2d_Curve class shows:
- how to work with the parametric equation of a curve in order to calculate the point of parameter u, together with the vector tangent and the derivative vectors of order 2, 3,..., N at this point;
- how to obtain general information about the curve (for example, level of continuity, closed characteristics, periodicity, bounds of the parameter field);
- how the parameter changes when a geometric transformation is applied to the curve or when the orientation of the curve is inverted. All curves must have a geometric continuity: a curve is at least "C0". Generally, this property is checked at the time of construction or when the curve is edited. Where this is not the case, the documentation explicitly states so. Warning The Geom2d package does not prevent the construction of curves with null length or curves which self-intersect.
Member Function Documentation
|
pure virtual |
It is the global continuity of the curve : C0 : only geometric continuity, C1 : continuity of the first derivative all along the Curve, C2 : continuity of the second derivative all along the Curve, C3 : continuity of the third derivative all along the Curve, G1 : tangency continuity all along the Curve, G2 : curvature continuity all along the Curve, CN : the order of continuity is infinite.
Implemented in Geom2d_BSplineCurve, Geom2d_BezierCurve, Geom2d_OffsetCurve, Geom2d_TrimmedCurve, Geom2d_Line, Geom2d_Conic, Bisector_BisecPC, Bisector_BisecCC, and Bisector_BisecAna.
|
pure virtual |
Returns in P the point of parameter U. If the curve is periodic then the returned point is P(U) with U = Ustart + (U - Uend) where Ustart and Uend are the parametric bounds of the curve.
Raised only for the "OffsetCurve" if it is not possible to compute the current point. For example when the first derivative on the basis curve and the offset direction are parallel.
Implemented in Geom2d_BSplineCurve, Geom2d_Hyperbola, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_OffsetCurve, Geom2d_Parabola, Bisector_BisecCC, Bisector_BisecPC, Geom2d_Line, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
Returns the point P of parameter U and the first derivative V1. Raised if the continuity of the curve is not C1.
Implemented in Geom2d_BSplineCurve, Geom2d_Hyperbola, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_OffsetCurve, Geom2d_Parabola, Bisector_BisecCC, Geom2d_Line, Bisector_BisecPC, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
Returns the point P of parameter U, the first and second derivatives V1 and V2. Raised if the continuity of the curve is not C2.
Implemented in Geom2d_BSplineCurve, Geom2d_Hyperbola, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_OffsetCurve, Geom2d_Parabola, Geom2d_Line, Bisector_BisecCC, Bisector_BisecPC, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
Returns the point P of parameter U, the first, the second and the third derivative. Raised if the continuity of the curve is not C3.
Implemented in Geom2d_BSplineCurve, Geom2d_Hyperbola, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_OffsetCurve, Geom2d_Parabola, Geom2d_Line, Bisector_BisecCC, Bisector_BisecPC, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
For the point of parameter U of this curve, computes the vector corresponding to the Nth derivative. Exceptions StdFail_UndefinedDerivative if:
- the continuity of the curve is not "CN", or
- the derivative vector cannot be computed easily; this is the case with specific types of curve (for example, a rational BSpline curve where N is greater than 3). Standard_RangeError if N is less than 1.
Implemented in Geom2d_BSplineCurve, Geom2d_Hyperbola, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_OffsetCurve, Geom2d_Parabola, Geom2d_Line, Bisector_BisecCC, Geom2d_Circle, Bisector_BisecPC, and Bisector_BisecAna.
|
pure virtual |
Returns the value of the first parameter. Warnings : It can be RealFirst or RealLast from package Standard if the curve is infinite.
Implemented in Geom2d_BSplineCurve, Geom2d_BezierCurve, Geom2d_OffsetCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_Hyperbola, Geom2d_Parabola, Geom2d_Line, Geom2d_Circle, Bisector_BisecPC, Bisector_BisecCC, and Bisector_BisecAna.
|
pure virtual |
Returns true if the curve is closed. Examples : Some curves such as circle are always closed, others such as line are never closed (by definition). Some Curves such as OffsetCurve can be closed or not. These curves are considered as closed if the distance between the first point and the last point of the curve is lower or equal to the Resolution from package gp wich is a fixed criterion independant of the application.
Implemented in Geom2d_BSplineCurve, Geom2d_OffsetCurve, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_Hyperbola, Bisector_BisecPC, Geom2d_Parabola, Bisector_BisecCC, Geom2d_Line, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
Returns true if the degree of continuity of this curve is at least N. Exceptions Standard_RangeError if N is less than 0.
Implemented in Geom2d_BSplineCurve, Geom2d_OffsetCurve, Geom2d_BezierCurve, Geom2d_TrimmedCurve, Geom2d_Line, Geom2d_Conic, Bisector_BisecPC, Bisector_BisecAna, and Bisector_BisecCC.
|
pure virtual |
Returns true if the parameter of the curve is periodic. It is possible only if the curve is closed and if the following relation is satisfied : for each parametric value U the distance between the point P(u) and the point P (u + T) is lower or equal to Resolution from package gp, T is the period and must be a constant. There are three possibilities : . the curve is never periodic by definition (SegmentLine) . the curve is always periodic by definition (Circle) . the curve can be defined as periodic (BSpline). In this case a function SetPeriodic allows you to give the shape of the curve. The general rule for this case is : if a curve can be periodic or not the default periodicity set is non periodic and you have to turn (explicitly) the curve into a periodic curve if you want the curve to be periodic.
Implemented in Geom2d_BSplineCurve, Geom2d_OffsetCurve, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_Hyperbola, Bisector_BisecPC, Geom2d_Parabola, Bisector_BisecCC, Geom2d_Line, Geom2d_Circle, and Bisector_BisecAna.
|
pure virtual |
Value of the last parameter. Warnings : It can be RealFirst or RealLast from package Standard if the curve is infinite.
Implemented in Geom2d_BSplineCurve, Geom2d_BezierCurve, Geom2d_OffsetCurve, Geom2d_Ellipse, Geom2d_TrimmedCurve, Geom2d_Hyperbola, Geom2d_Parabola, Geom2d_Line, Geom2d_Circle, Bisector_BisecPC, Bisector_BisecCC, and Bisector_BisecAna.
|
virtual |
Returns the coefficient required to compute the parametric transformation of this curve when transformation T is applied. This coefficient is the ratio between the parameter of a point on this curve and the parameter of the transformed point on the new curve transformed by T. Note: this function generally returns 1. but it can be redefined (for example, on a line).
Reimplemented in Geom2d_OffsetCurve, Geom2d_TrimmedCurve, Geom2d_Parabola, and Geom2d_Line.
|
virtual |
Returns thne period of this curve. raises if the curve is not periodic.
Reimplemented in Geom2d_OffsetCurve, and Geom2d_TrimmedCurve.
|
pure virtual |
Changes the direction of parametrization of <me>. The "FirstParameter" and the "LastParameter" are not changed but the orientation of the curve is modified. If the curve is bounded the StartPoint of the initial curve becomes the EndPoint of the reversed curve and the EndPoint of the initial curve becomes the StartPoint of the reversed curve.
Implemented in Geom2d_BSplineCurve, Geom2d_BezierCurve, Geom2d_OffsetCurve, Geom2d_Conic, Geom2d_Line, Geom2d_TrimmedCurve, Bisector_BisecPC, Bisector_BisecAna, and Bisector_BisecCC.
| Handle< Geom2d_Curve > Geom2d_Curve::Reversed | ( | ) | const |
Creates a reversed duplicate Changes the orientation of this curve. The first and last parameters are not changed, but the parametric direction of the curve is reversed. If the curve is bounded:
- the start point of the initial curve becomes the end point of the reversed curve, and
- the end point of the initial curve becomes the start point of the reversed curve.
- Reversed creates a new curve.
|
pure virtual |
Computes the parameter on the reversed curve for the point of parameter U on this curve. Note: The point of parameter U on this curve is identical to the point of parameter ReversedParameter(U) on the reversed curve.
Implemented in Geom2d_BSplineCurve, Geom2d_BezierCurve, Geom2d_Ellipse, Geom2d_Hyperbola, Geom2d_OffsetCurve, Geom2d_Parabola, Geom2d_Conic, Geom2d_Line, Geom2d_TrimmedCurve, Geom2d_Circle, Bisector_BisecPC, Bisector_BisecAna, and Bisector_BisecCC.
|
virtual |
Computes the parameter on the curve transformed by T for the point of parameter U on this curve. Note: this function generally returns U but it can be redefined (for example, on a line).
Reimplemented in Geom2d_OffsetCurve, Geom2d_TrimmedCurve, Geom2d_Parabola, and Geom2d_Line.
| gp_Pnt2d Geom2d_Curve::Value | ( | const Standard_Real | U | ) | const |
Computes the point of parameter U on <me>. If the curve is periodic then the returned point is P(U) with U = Ustart + (U - Uend) where Ustart and Uend are the parametric bounds of the curve.
it is implemented with D0.
Raised only for the "OffsetCurve" if it is not possible to compute the current point. For example when the first derivative on the basis curve and the offset direction are parallel.
The documentation for this class was generated from the following file:
 1.8.10
1.8.10